Table of Contents
Vertical Circular Motion
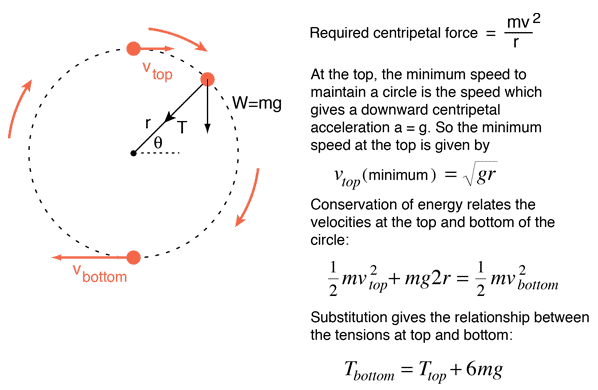
| For vertical circular motion, the motion is not uniform, as the object increases speed on the downward swing and |
| decreases on the way up. When analyzing vertical circular motion, one finds that there are two forces acting on the |
| object. These two forces are T, the tension in the string, and FW, the weight of the object, as shown below. |
 |
| The weight, FW, can be resolved into a tangential component expressed as FWsinθ and a radial component expressed |
| as FWcosθ. Applying Newton’s second law to express the tangential acceleration gives: |
|
aT = FT/m = FWsinθ/m = |
| Similarly, the radial acceleration can be expressed as: |
|
aR = FR/m = (T – FWcosθ)/m = (T – mgcosθ)/m |
| Substituting v2/r for aR and solving for T yields: |
|
T = m(v2/r + gcosθ) |
| Two interesting points to consider are the top and the bottom of the circle. First the bottom: |
| At the lowest point of the circular path, θ = 0° and cos 0° = 1. Substituting into the equation for T yields: |
|
T = m(v2/r + g) |
| At the highest point of the circular path, θ = 180° and cos 180° = -1. Substituting into the equation for T yields: |
|
T = m(v2/r – g) |
| At both the highest and lowest point, the tangential acceleration is zero because sin 0° = sin 180° = 0 and the |
| acceleration is strictly radial. Physically at these two points, could there be similarities between being on an elevator |
| and being on a ferris wheel? |
| At the top of a vertical circle, there are two possible forces that can exist: FW – the weight of the object, and FT – the |
| tension in the string. The simulator solves problems assuming the only force at the top is FW. It assumes that the weight |
| is the only agent providing the centripetal force which represents the minimum speed the mass must have. At any smaller |
| velocity, the string does not remain taught and the mass falls out of its circular path. |
| The x and y velocity components are displayed to further show that circular motion is as sinusoidal as a pendulum. Just |
| as with the Horizontal Circular Motion simulator, after entering the input values, press Play and the remaining values will |
| be computed. The simulator accepts simple factors for entries. For example, if a problem gives the weight of an object |
| (685 N) rather than its mass, simply enter 685/9.80 for its mass. |
| 1) A man with a mass of 75 kg rides on a ferris wheel which is 21.5 m in diameter and rotates once every 14.0 s. |
| (a) How much would the man appear to weigh at the top of the ferris wheel? |
| (b) How much would the man appear to weigh at the bottom of the ferris wheel? |
| 2) A motorcyclist rides down a ramp and around the loop-the-loop as shown below. If the loop has a radius of 17 m, |
| what is the slowest speed the rider can have at the top of the loop to avoid falling? |
 |
| 3) A 80.0 kg person is spinning around the equator of a planet which is rotating at 3.2 x 103 km/h. The centripetal force |
| present is 8.0 N. What is the radius of the planet? |
| 4) An object with a mass of 8.0 kg is swung in a vertical circle of radius 2.4 m with a speed of 6.0 m/s. |
| (a) Determine the maximum and minimum tension in the string. |
| (b) The string breaks when the tension exceeds 340 N. Determine the maximum speed of the mass and where the |
| mass will be when the string breaks. Justify your answer as to where the mass will be. |
|
CF Solver |