Table of Contents
Introduction To Circular Motion
| To consider some of the “real-life” applications, those involving friction and the weight of the object, don’t forget to |
| check out the Horizontal Circular Motion simulator. |
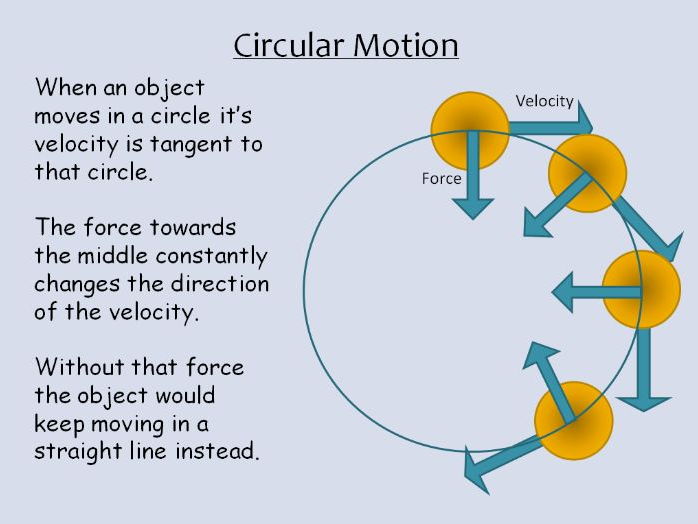
| Newton’s first law states that in the absence of a net force, an object will continue to move in a straight line indefinitely at |
| constant speed. However, a net force applied in the direction of the velocity will cause an object to speed up and |
| when applied in the opposite ditrection, the object slows down. In these two cases, the net force causes a change in the |
| speed of the object. A third case is when the net force is perpendicular to the velocity vector. In this case, the object |
| continues at a constant speed but follows a circular path. In such a case, the net force (called the centripetal force) is |
| directed towards the center of the circle. In accordance with Newton’s second law, the acceleration is also directed to |
| the center of the circle and is appropriately called the centripetal acceleration. |
| The formulas used in UCM (uniform circular motion) are: |
|
acp = v2/r and Fcp = mv2/r |
| and as always units are important. The mass, m, must be in kg, the velocity, v, must be in m/s, and the radius, r, must be |
| in meters. We will restrict the motion of the object to that of a horizontal circle, i.e. a circle parallel to the ground as on a |
| merry-go-round. |
| What may not be intuitively obvious to the most casual observer is that circular motion and rotary motion are not totally |
| different from each other. Both are examples of periodic motion where periodic motion is that type of motion that is |
| repeated at equal time intervals. The time needed for a complete interval is called the period. This relationship can be |
| expressed in the following formulas: |
|
v = C/T = 2πr/T and a = 2πv/T |
| where C is the circumference of the circle in m and T is the time needed for one revolution (period) measured in s. |
| The appropriate rotary quantities are expressed as: |
|
s = rθ and v = rω |
| where s is the linear displacement measured in m, r is the radius in m, θ is the angular displacement in radians (rad), and |
| ω is the angular velocity in rad/s. |
| The simulator accepts simple factors for entries. For example, if a problem gives the weight of an object (685 N) rather |
| than its mass, simply enter 685/9.80 for its mass. |
| Unlike some of the other animations, you must enter your inputs before pressing Play. |
| 1) Assume the circle in the animation has a radius of 2.0 m and a 5.0 kg mass is being swung in a horizontal circle. |
| (a) What is the time for one complete revolution? |
| (b) What is the magnitude and direction of the velocity for the 5.0 kg mass? |
| (c) What is the direction of the acceleration? Does the acceleration remain constant? Explain your answer. |
| (d) What is the magnitude and direction of the centripetal force? |
| 2) The newest Rolex watch has a second hand which is 2.2 cm long. |
| (a) Determine the speed of the tip of the second hand. |
| (b) Compare the velocity of the tip of the second hand as it passes over the 12 with that of the 9. |
| 3) Apply Newton’s 3rd law to Problem 1 above. When the string exerts a force of 40. N on the 5.0 kg mass, the |
| centripetal force can be considered as the action force. What is the reaction force in this problem? You probably |
| have heard this force referred to as the centrifugal force. Why don’t these two forces, the centripetal and the |
| centrifugal force cancel out leaving Fnet = 0.? Justify your reasoning. |
|
CF Solver |